In some ways Norton's Theorem can be thought of as the opposite to "Thevenins Theorem", in that Thevenin reduces his circuit down to a single resistance in series with a single voltage. Norton on the other hand reduces his circuit down to a single resistance in parallel with a constant current source. Norton's Theorem states that "Any linear circuit containing several energy sources and resistances can be replaced by a single Constant Current generator in parallel with a Single Resistor". As far as the load resistance, RL is concerned this single resistance, RS is the value of the resistance looking back into the network with all the current sources open circuited and IS is the short circuit current at the output terminals as shown below. The value of this "Constant Current" is one which would flow if the two output terminals where shorted together while the source resistance would be measured looking back into the terminals, (the same as Thevenin). For example, consider our now familiar circuit from the previous section. To find the Nortons equivalent of the above circuit we firstly have to remove the centre 40O load resistor and short out the terminals A and B to give us the following circuit. When the terminals A and B are shorted together the two resistors are connected in parallel across their two respective voltage sources and the currents flowing through each resistor as well as the total short circuit current can now be calculated as: If we short-out the two voltage sources and open circuit terminals A and B, the two resistors are now effectively connected together in parallel. The value of the internal resistor Rs is found by calculating the total resistance at the terminals A and B giving us the following circuit. Having found both the short circuit current, Is and equivalent internal resistance, Rs this then gives us the followingNortons equivalent circuit. Ok, so far so good, but we now have to solve with the original 40O load resistor connected across terminals A and B as shown below. Again, the two resistors are connected in parallel across the terminals A and B which gives us a total resistance of: The voltage across the terminals A and B with the load resistor connected is given as: Then the current flowing in the 40O load resistor can be found as: which again, is the same value of 0.286 amps, we found using Kirchoff's circuit law in the previous tutorials. The basic procedure for solving Nortons Analysis equations is as follows: Thevenins Theorem : states that "Any linear circuit containing several voltages and resistances can be replaced by just a Single Voltage in series with a Single Resistor". In other words, it is possible to simplify any "Linear" circuit, no matter how complex, to an equivalent circuit with just a single voltage source in series with a resistance connected to a load as shown below. Thevenins Theorem is especially useful in analyzing power or battery systems and other interconnected circuits where it will have an effect on the adjoining part of the circuit. As far as the load resistor RL is concerned, any "One-port" network consisting of resistive circuit elements and energy sources can be replaced by one single equivalent resistance Rs and voltage Vs, where Rs is the source resistance value looking back into the circuit and Vs the open circuit voltage at the terminals. For example, consider the circuit from the previous section. Firstly, we have to remove the centre 40O resistor and short out (not physically as this would be dangerous) all the emf�s connected to the circuit, or open circuit any current sources. The value of resistor Rs is found by calculating the total resistance at the terminals A and B with all the emf�s removed, and the value of the voltage required Vs is the total voltage across terminals A and B with an open circuit and no load resistor Rs connected. Then, we get the following circuit. We now need to reconnect the two voltages back into the circuit, and as VS = VAB the current flowing around the loop is calculated as: so the voltage drop across the 20O resistor can be calculated as: VAB = 20 - (20O x 0.33amps) = 13.33 volts. Then the Thevenins Equivalent circuit is shown below with the 40O resistor connected. and from this the current flowing in the circuit is given as: which again, is the same value of 0.286 amps, we found using Kirchoff�s circuit law in the previous tutorial. Thevenins theorem can be used as a circuit analysis method and is particularly useful if the load is to take a series of different values. It is not as powerful as Mesh or Nodal analysis in larger networks because the use of Mesh or Nodal analysis is usually necessary in any Thevenin exercise, so it might as well be used from the start. However, Thevenins equivalent circuits of Transistors, Voltage Sources such as batteries etc, are very useful in circuit design. The basic procedure for solving Thevenins Analysis equations is as follows: Superposition theorem is one of those strokes of genius that takes a complex subject and simplifies it in a way that makes perfect sense. The strategy used in the Superposition Theorem is to eliminate all but one source of power within a network at a time, using series/parallel analysis to determine voltage drops (and/or currents) within the modified network for each power source separately. Then, once voltage drops and/or currents have been determined for each power source working separately, the values are all �superimposed� on top of each other (added algebraically) to find the actual voltage drops/currents with all sources active. Let�s look at our example circuit and apply Superposition Theorem to it:Norton's Theorem:
Norton's equivalent circuit.


with A-B Shorted Out
Find the Equivalent Resistance (Rs)
Nortons equivalent circuit.


Nortons Analysis Summary.
Thevenins equivalent circuit.



Find the Equivalent Resistance (Rs)

Find the Equivalent Voltage (Vs)




Summary.
Superposition Theorem:
Since we have two sources of power in this circuit, we will have to calculate two sets of values for voltage drops and/or currents, one for the circuit with only the 28 volt battery in effect. . .
. . . and one for the circuit with only the 7 volt battery in effect
When re-drawing the circuit for series/parallel analysis with one source, all other voltage sources are replaced by wires (shorts), and all current sources with open circuits (breaks).
Analyzing the circuit with only the 28 volt battery

Analyzing the circuit with only the 7 volt battery

Super Imposing Voltage
Super Imposing current
Final Circuit
REVIEW
The Superposition Theorem states that a circuit can be analyzed with only one source of power at a time, the corresponding component voltages and currents algebraically added to find out what they�ll do with all power sources in effect.
To negate all but one power source for analysis, replace any source of voltage (batteries) with a wire; replace any current source with an open (break).
all about electronic device
Popular Posts
-
The critical part of the fm radio receiver is the first stage, TR1/VC1, where the wirings must be kept as short as possible. Coil L1 is form...
-
WorldWide Tech & Science. Francisco De Jes�s. Austrian Felix Baumgartner jumps from a balloon 24 miles above Earth. Video. Austrian da...
-
WorldWide Tech & Science. Francisco De Jes�s. NETGEAR Executives Discuss Future of Connectivity and Storage at Key January Conferences. ...
-
WorldWide Tech & Science. Francisco De Jes�s. South Korea: LG takes on the iPhone 5 on newspaper ad. A newspaper advertisement b...
-
A bread board is also known as a project board, It has got itself a place in every electronics hobbyist because of its "User Friendly...
-
WorldWide Tech & Science. Francisco De Jes�s. CES2013: Download the app for your mobile. USA and Canada only. You can download th...
-
Switzerland's telecom service provider Swisscom is currently testing the LTE in Grenchen. According to the company statement, LTE is t...
-
WorldWide Tech & Science. Francisco De Jes�s. GMail v2.0 for iPhone and iPad is out. Description Get the official Gmail app for your iPh...
-
WorldWide Tech & Science. Francisco De Jesùs. Ecuador to launch its first satellite "Pegasus". Students desks will become spa...
Blog Archive
-
▼
2011
(66)
-
▼
January
(30)
- DTMF (Dual-tone multi-frequency )
- ELECTRONIC SOFTWARES & BOOKS FREE DOWNLOAD
- DIODES
- SWITCHES
- BREAD BOARD
- LIGHT DEPENDENT RESISTORS(LDR)
- LIGHT SENSITIVE ALARM
- LED TORCH USING MAX660
- SIMPLE LIE DETECTOR
- SIMPLE FM RECEIVER WITH EAR PHONES
- MOBILE PHONE CHARGER
- WIRELESS SWITCH
- LASER ACTIVATED SWITCH
- RADIO WAVES DETECTOR
- FREE PCB DESIGN SOFTWARE
- MISCELLANEOUS ELECTRONICS SOFTWARE
- FM TRANSMITTERS (SIMPLE DESIGNS)
- TRANSFORMERS
- TOUCH SWITCH
- SIMPLEST RADIO
- AIR CRAFT RADIO COMMUNICATION RECEIVER
- K- MAPS SOFTWARE AND INTRODUCTION(karnaughs maps)
- SR-FLIP FLOP
- NETWORK THEOREMS
- UNI JUNCTION TRANSISTOR
- BIPOLAR JUNCTION TRANSISTOR (BJT)
- FIELD EFFECT TRANSISTOR (FET)
- SILICON CONTROLLED RECTIFIER (SCR)
- JFET
- MOSFET
-
▼
January
(30)
About Us
Hi world! I'm an enthusiast blogger within passion in electronics field.
Footer Widget 2
Footer Widget 3
Copyright © 2011 what is electronics | Powered by Blogger
Design by Free WordPress Themes | Bloggerized by Lasantha - Premium Blogger Themes | Eagle Belt Buckles




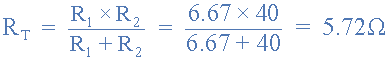









0 comments:
Post a Comment